Bild 1Z.u.L. > Dokumentation > Probleme
Ich möchte hier auf typische Probleme hinweisen, die mir und anderen Anwendern aufgefallen sind. Es handelt sich um typische Fehler, die immer wieder gemacht werden, und die wohl jeder antreffen wird, der mit Z.u.L. oder einem anderen dynamischen Geometrieprogramm eine Gruppe von Schülern unterrichtet.
Ich habe versucht, viele diese Fallstricke durch geschicktes Design der Programmoberfläche zu entschärfen, was oft mit einfachen Maßnahmen möglich war. Mein Aufruf geht aber an alle Lehrer und Anwender, mir Probleme zu mitzuteilen, die bei ihnen auftraten. Oft fließen die Rückmeldungen und Ideen der Benutzer schon in die nächste Version ein.
I. Falsche Vorstellung von "Konstruktion"
II. Überschätzung des Programms
III. Mehrere Kreiswerkzeuge
IV. Mehrere Schnittpunkte
V. Allgemeingültige Konstruktionen
Natürlich weise ich im Tutorium darauf hin, dass neue Punkte als Schnittpunkte konstruiert werden müssen, wenn ihre Lage nicht beliebig sein darf. Aber ebenso natürlich übertragen immer wieder Anwender Konstruktionen inkorrekt von der Tafel auf den Computer.
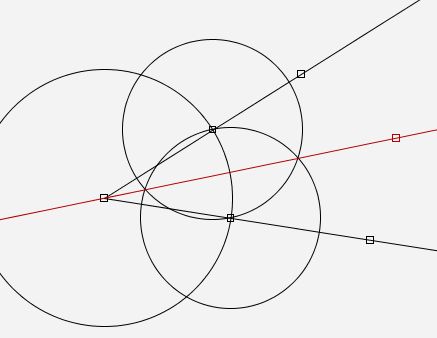
Der folgende Versuch einer Konstruktion der Winkelhalbierenden zeigt den typischen Fehler.
Bild 1
Es geht um die rote Gerade. Offenbar wurde der rote Punkt so gesetzt, dass die Gerade visuell durch den Schnittpunkt der beiden Kreise geht, anstatt den Schnittpunkt der Kreise zu erzeugen und die Gerade durch diesen Schnittpunkt gehen zu lassen. Ein Verschieben der Ausgangspunkte würde den Fehler natürlich sofort entlarven.
Die Gerade wurde gewissermaßen in Analogie zum Konstruieren mit dem Lineal gesetzt. Das Lineal wird nämlich genau mit dieser "Peilmethode" verwendet. Geometrieprogramme besitzen aber eine andere Logik.
Um den Fehler zu vermeiden, genügt es, die Vorschau von erzeugten Objekten abschalten, wie es beim Anfängermodus von Z.u.L. der Fall ist. Dann ist die Gerade erst sichtbar, wenn Ihre Endpunkte gesetzt wurden.
Eine noch strengere Alternative wäre, immer erst die Erzeugung von Punkten zu fordern, bevor Geraden durch diese Punkte gelegt werden können. Mir erscheint ein solch umständlicher Modus aber nicht nötig zu sein. Der Anfängermodus genügt vollkommen, um das Problem zu vermeiden.
Nachdem der Benutzer sich erst einmal daran gewöhnt hat, dass er mit einem Geometrieprogramm mehr machen kann als mit dem Zirkel und dem Lineal, fängt er sofort an, Dinge zu verlangen, die das Programm nicht leisten kann.
Ein typisches Beispiel ist die Aufgabe, ein Dreieck mit drei gegebenen Seitenlängen zu konstruieren. Nun lässt sich in Z.u.L. eine Strecke in der Länge fixieren. Demgemäß konstruieren Anwender ein beliebiges Dreieck und versuchen die Seiten auf eine bestimmte Länge zu fixieren. Das ist eine Idee, die mit realen Instrumenten niemals aufkommen würde. Und in der Tat verweigert Z.u.L. bei der dritten Seite die Fixierung.
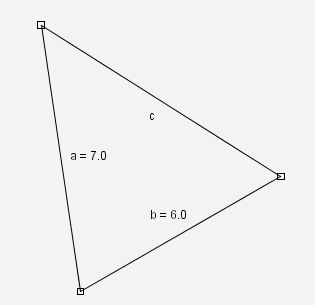Bild 2
Ein anderes Beispiel entsteht, wenn man vergisst, dass die Konstruktionsschritte voneinander abhängig sind.
In der folgenden Konstruktion wird die Aufgabe gestellt, A so auf dem Kreis zu wählen, dass die Mitte M der Strecke PA auf dem Kreis liegt. A ist an den Kreis gebunden. Die simple Idee ist nun zu versuchen, auch M an den Kreis zu binden. Z.u.L. lässt das natürlich nicht zu, weil es sonst zu Wechselwirkungen bei den Abhängigkeiten kommen würde.
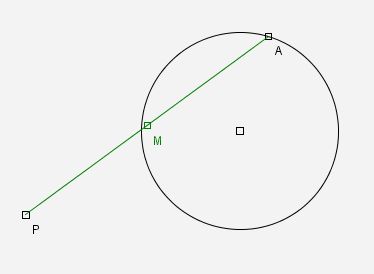Bild 3
Genauso inkorrekt ist natürlich, A so zu verschieben, dass M zufällig auf dem Kreis liegt. Auch dieser Betrug entlarvt sich, wenn der Punkt P oder der Kreis verschoben wird.
Es gibt in Z.u.L. drei Werkzeuge, um Kreise zu erzeugen.
Bild 4
Beim ersten Kontakt mit dem Programm wählen fast alle Benutzer das falsche aus. Um wenigstens deutlich zu machen, dass es drei Möglichkeiten gibt, sind die Werkzeuge in neueren Versionen von Z.u.L. nebeneinander angeordnet.
Man muss zugeben, dass das mittlere Werkzeug am ehesten dem entspricht, was man vom Zirkel her gewohnt ist. Man misst eine Strecke mit dem Zirkel ab und zeichnet an einem anderen Punkt einen Kreis.
Das linke Werkzeug entspricht dem so genannten "kollabierenden" Zirkel. Dieser Zirkel verliert seine Einstellung, wenn er vom Papier entfernt wird. Im Tutorium wird gezeigt, wie man den normalen Zirkel mit diesem Zirkel ersetzen kann. Natürlich kann man umgekehrt auf dieses Werkzeug ganz verzichten, und der Lehrer mag es aus dem Werkzeugsatz entfernen, wenn er das für richtig hält.
Das rechte Werkzeug erzeugt Kreise, deren Radius durch eine Zahl fixiert ist. Es entspricht also einem Zirkel, den man auf einen bestimmten Radius einstellen kann, bzw. einer Kombination aus Messlineal und Zirkel. Drastischer wirkt sich das Werkzeug aus, wenn man Ausdrücke für den Kreisradius verwendet. Dann entstehen virtuelle Konstruktionen, die kein Gegenstück in realen Konstruktionen haben.
Anwender benutzen das Werkzeug weit häufiger als ich selbst. Die Folge ist, dass die folgende Konstruktion der Mittelsenkrechten ungültig wird, wenn A und B auseinander geschoben werden.
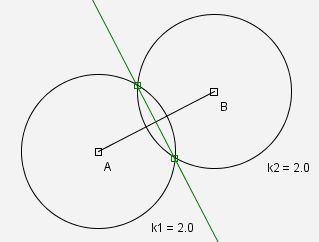Bild 5
Korrekt ist natürlich, Kreise um A durch B und um B durch A zu benutzen.
Bei der Konstruktion der Winkelhalbierenden (wie in Bild 1) ist es ebenfalls unnötig, mit einem festen Kreis zu starten. Sinnvoll ist ein Kreis um den Schenkelpunkt und durch einen Punkt auf einem der Strahlen.
Zusammengefasst bleibt die Kreisproblematik ein erklärungsbedürftiger Punkt in der Bedienung von Geometriesoftware.
Z.u.L. scheint automatisch den richtigen Schnittpunkt zweier Kreise zu wählen, nämlich den, den der Benutzer beim Erzeugen angeklickt hat. Werden die Kreise bewegt oder in der Größe verändert, so wird der Schnittpunkt stetig mitbewegt, solange zwei wohldefinierte Schnittpunkte existieren. So sollte es ja auch sein.
Geht man allerdings beim Verändern über Sonderfälle, also keine Schnittpunkte, deckungsgleiche Kreise, tangential berührende Kreise oder Kreise mit Radius 0, so ist das Ergebnis nicht so klar. In Z.u.L. gilt immerhin die Regel, dass gleiche Konstellationen immer denselben Schnittpunkt auswählen. Andere Programme ändern die Auswahl beim Bewegen.
Das hat aber zur Folge, dass das Abtragen von Winkeln mittels kongruenten Dreiecken nicht richtig funktioniert.
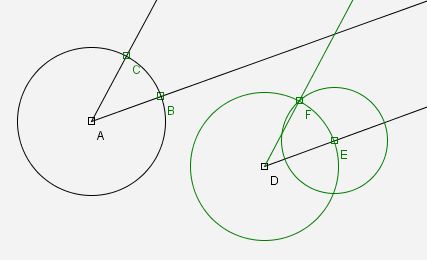Bild 6
Der Winkel BAC ist an den Strahl DE anzutragen. Man nimmt dazu den abtragenden Zirkel und trägt AB bei D ab, und man erhält E. Schließlich trägt man BC bei E an und erhält F. Da ABC und DEF drei gleiche Seiten haben, sind BAC und EDF kongruent.
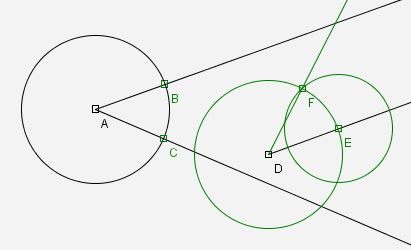Bild 7
Leider funktioniert diese Konstruktion nicht mehr, wenn man C unter halb von B verschiebt. Der Winkel wird immer nach oben abgetragen, weil die beiden grünen Kreise ja immer noch in derselben Lage sind. Beim Bewegen von C geht der kleinere grüne Kreis über einen Zustand, bei dem er den Radius 0 hat.
Will man wirklich einen orientierten Winkel abtragen, so kann man in Z.u.L. feste Winkel verwenden, muss aber die Beschränkung auf 180 Grad abschalten. Als Ausdruck müsste man a(D,A,C) eingeben. Im Dialog für feste Winkel kann man den Ausdruck für den Winkel interaktiv durch Auswahl der Punkte B, A und C festlegen.
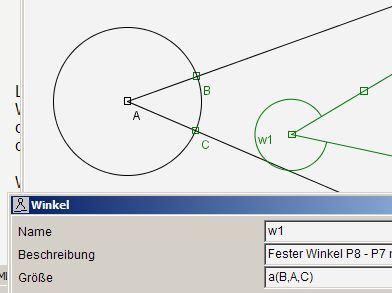Bild 8
Ein anderer Fall, bei dem die Auswahl des Schnittpunktes eine Rolle spielt, ist die Spiegelung an einer Geraden. Die normale Konstruktion geht mit Hilfe des Lots von P auf die Gerade und einem Kreis um den Fußpunkt F durch P. P* ist dann der andere Schnittpunkt des Kreises mit dem Lot.
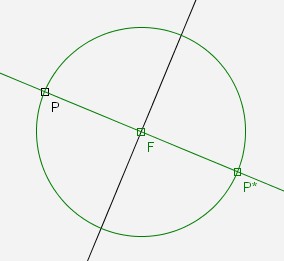Bild 9
Diese Konstruktion wäre nicht allgemeingültig, wenn es nicht eine Automatik gäbe, der den Schnitt P* so auswählt, dass er verschieden von P ist. Zieht man nämlich den Punkt P auf die andere Seite der Gerade, so würde P* mit P zusammenfallen. Die erwähnte Automatik verhindert dies. Wenn einer der Schnittpunkte (hier P) schon bekannt und sichtbar ist, geht das Programm davon aus, dass der Benutzer immer den anderen Schnittpunkt (hier P*) will und setzt einen entsprechenden Schalter. Man kann das im Eigenschaftsdialog von P* abschalten.
Der Grund dafür ist, dass die Orientierung des Lots sich nach der Orientierung der Geraden richtet, und nicht nach der Seite, auf der P liegt. Der Kreis hat keine Orientierung. Daher würde P* ohne den Schalter immer auf derselben Seite der Geraden liegen.
Man kann sich hier damit behelfen, dass man eine neue Gerade PF erzeugt und den Kreis mit dieser Geraden schneidet, die ja dann immer so orientiert ist, dass sie von P zur Spiegelgeraden zeigt.
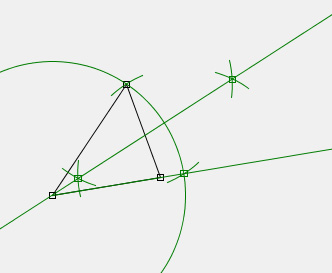
Manche Konstruktionen sehen in der gegebenen Konfiguration korrekt aus. Wenn sich die Ausgangslage verschiebt, werden sie aber falsch. Die Ursache sind fast immer falsch oder gar nicht konstruierte Schnittpunkte. Neben den schon erwähnten Problemen gibt es ein weiteres Problem.
Schnittpunkte werden nämlich ungültig, wenn sich die Objekte nicht mehr schneiden. Diese banale Feststellung gilt auch für Strecken und Kreise. Aus diesem Grund sollte man zum Beispiel bei der Konstruktion der Winkelhalbierenden von Strahlen ausgehen und nicht von Strecken. Notfalls muss ein Hilfsstrahl oder eine Hilfsgerade entlang der Dreiecksseiten erzeugt werden.
Bild
10
Die Alternative ist im Eigenschaftsdialog der Schnitte "Eingeschränkt" abzustellen.
Das gleiche gilt für Lote auf Strecken.
Z.u.L. > Dokumentation > Probleme